| More Examples |
| Explanation of Notation |
| How does it work? |
Haar Transform
The Haar transform, HT, is defined recursively by:
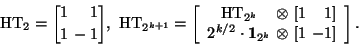
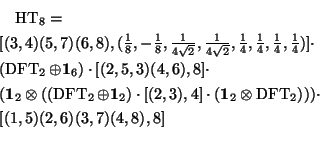
O.k., you where not looking for math, but hoping to find good code for this (or other) transforms? No problem, get SPIRAL.

|
Haar TransformThe Haar transform, HT, is defined recursively by: 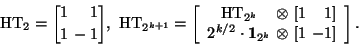 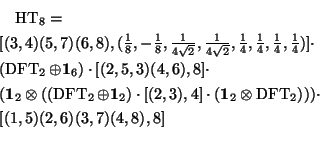 O.k., you where not looking for math, but hoping to find good code for this (or other) transforms? No problem, get SPIRAL. |